Introduction to |
|
CONTACT: info.snaranan@gmail.com |
© Copyright 2011
Prof. S. Naranan
Chennai 600041, INDIA
Universal Calendar
ABSTRACT
The Universal Calendar is used primarily for finding the weekday of any given date (day, month, year). The Universal Calendar for the 21st century (2000-2099) is given as Figure 1 on page 2. It contains three short tables. The procedure for finding the date is given on page 3. The same calendar with some modifications can be used for other centuries too. See page 4, for its usage in 20th, 22nd, 23rd and 24th centuries. There is a 400-year cycle in the calendar; e.g. the calendar for the years 2011 and 2411 are the same. Some additional information about the calendar (the Julian-Gregorian) are given in pages 5 and 6 with some illustrative examples.
Note: The paper "The Calendar Problems" may
be read as a companion paper. It deals with some elementary mathematics which forms the basis for the Universal Calendar Chart presented in this paper.
| The Universal Calendar | Page 2 |
| How to use the Universal Calendar | Page 3 |
| Extension of Universal Calendar for other centuries | Page 4 |
| Additional Notes on the Universal Calendar | Pages 5, 6 |
Note: For easy comprehension of material in the pages 3, 4, 5, 6 it
is desirable to have a printout of the universal calendar (page 2) for quick reference.
Page 2
An Universal Calendar
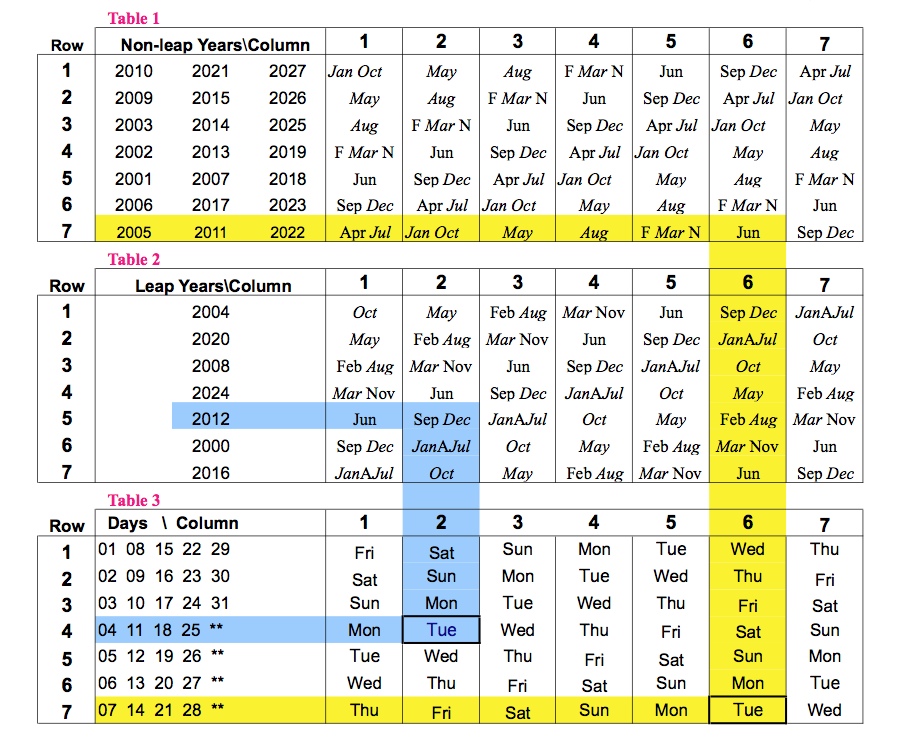
Figure 1
Page 3
How to use the Universal Calendar?
This Universal Calendar can be used to find the Weekday of any Date (Year Y, Month M, Day D) in the 21st century (2000-2099). Table 1 is used for non-leap years and Table 2 for the leap years. In Table 1 F is Feb and N is Nov. In Table 2, A is Apr. The months with 31 days are shown in italics.
There is a 28-year cycle in the calendar for any given century. The calendar for the years 2000, 2028, 2056, 2084 are the same. So the calendar displays only the years 2000-2027.
Divide the last two digits of the year by 28 and take the remainder as Y.
Find the row in Table (1 or 2) corresponding to the year. In that row find the column in which the month (M) occurs. Go down the column to Table 3. In the column find the row in which the day (D) occurs. The row and column gives the day corresponding to the date.
Example: Find the weekday of 14 Jun 2011. In Table 1, 2011 Jun corresponds to row 7 and column 6. In Table 3, column 6 and row 7 (for the day 14) give the weekday as TUE (highlighted in yellow).
Example: Find the weekday of 25 Dec 2096. Dividing 96 by 28, the
remainder is 12. In Table 2, 2012 Dec corresponds to row 5 and column 2 . In Table 3, column 2 and row 4 (for the day 25) give the weekday as TUE (highlighted in blue).
Page 4
Extension of Universal Calendar for other Centuries:
The same Calendar (21 st century) can be used for other centuries with a slight modification. First, the relevant column in Tables 1, 2 for a given date, is determined as on page 3. Second, this column number is increased by a quantity x depending on the century. The value of x is 1, 5, and 3, respectively for the 20th, 22nd and 23rd centuries. If the increment leads to a number greater than 7, then 7 is subtracted to keep the column number 1 to 7. The above changes are spelt out in detail in the following paragraphs.
(1) For the 20th century (1900-1999): In Tables 1 and 2, the first two digits of the year "20" will be replaced by the first two digits of the century ("19"). E.g. to find the weekday of 4 Jul 1947: 1947 is equivalent to 1919 which is in row 4 of Table 1. In this row Jul is in column 4.
NOW ADD 1 TO THE COLUMN NUMBER. If the result exceeds 7, subtract 7. Column 4 becomes column 5. Going down column 5 to Table 3, row 4 (4th) gives the day as FRI.
(2) For the 22nd century (2100-2199): Proceed as for the 20th century, except that the column number is increased by 5. E.g. 4 Jul 2147 will correspond to column 2 (=4+5-7). Going down column 2 to Table 3, row 4 (4th) gives the day as TUE.
(3) For the 23rd century (2200-2299): Proceed as for the 20th century, except that the column number is increased by 3. E.g. 4 Jul 2247 will correspond to column 7 (=4+3). Going down column 7 to Table 3, row 4 (4th) gives the day as SUN.
(4) For the 24th century (2300-2399): The Calendar is the same as for the
20th century (1900-1999) because of the 400-year cycle for the Julian
Calendar.
CAUTION: The centesimal years 1900, 2100, 2200, 2300 are not leap years
unlike the year 2000. So, these years will be shifted from Table 2, row 6
to the same row (#6) in Table 1. For example to find the weekday of 1 Jan 1900, Table 1 (row 6)
has Jan in column 3. Adding one we get column 4. Going down column 4 in Table 3 gives 1 Jan 1900 as MON.
Page 5
Additional notes on the Universal Calendar
The Julian Calendar, established by Julius Caesar in 46 B.C had 12 months in a year,
each month with 31 or 30 days, except Feb which had 28 days. The year had 365 days. But every fourth year
Feb had 29 days; these years - called leap years - were exact multiples of 4. To correct an error in the
Julian Calendar, Pope Gregory XII modified the "leap year" rule: an year ending
in "00" - the centesimal year - is a leap year only if it is a multiple of 400. This
was introduced in 1582 in Great Britain and the American Colonies in 1752. Among the centesimal years
so far, only 1600 and 2000 have been leap years. Calendar problems are interesting mainly because of
two features: (1) the varying length of the months (31, 30, 28/29 days) and (2) the leap year rules.
The primary purpose of the Universal Calendar is to find the weekday
corresponding to a given date (day, month, year). But it can be used for other purposes too. We give a few examples.
(1) In which month/s does Fri 13th occur in 2011?
In Table 3, Fri 13th is in column 3. Moving up in column 3 to Table 1 (row 7) for 2011, gives the month as May. Note that same is true for the years 2005 and 2022.
(2) In which month/s in 2011 are five Fri,Sat,Sun?
This can happen only in months with 31 days, when the first day of the month is Fri. In
Table 3 Fri 1st is in column 1. Moving up column 1 to Table 1 (row 7) for 2011, gives the months as Apr and Jul. But
only Jul has 31 days. So Jul 2011 has 5 Fri, Sat, Sun.
Page 6
(3) Can five Fri, Sat, Sun occur in two different months in the same year?
Moving up in column 1 (corresponding to Fri 1st in Table 3), to Table 1 there are only two 31-day months (Jan, Oct) in the years 2010, 2021, 2027 (row 1). In Table 2, column 1 has two 31-day months (Jan, Jul) in 2016 (row 7). The answer is yes.
(4) In which leap year is Xmas day a Sunday?
In Table 3, Sun 25th is in column 7. Moving up in column 7 to Table 2, Dec (row 7) gives the year as 2016.
(5) When is leap Sunday?
29th Feb is a Sun in the year 2004.
(6) In which year/s are there 53 Sun?
The 53rd Sun can only be 31 Dec. Additionally it can be on 30 Dec., in leap years.
So the answer is:
2006, 2017 and 2023 (non-leap years) and 2000, 2012 (leap years).
(7) Can Fri 13th occur in a month with five Fridays?
Every month has four full weeks and a fifth week of upto 3 days. The fifth Fri can only be 29th, 30th or 31st day of a month. None of these differ from 13 by a multiple of 7. So there is no Fri 13 in a month with five Fri. Note this solution did not require the Universal Calendar!
S. Naranan
Chennai, India
6 Aug 2011
Brief Bio:
Dr. S. Naranan (b. 1930) was an experimental cosmic-ray physicist and X-ray Astronomer based mostly in the Tata Institute of Fundamental Research (TIFR), Bombay, India, in a career spanning 42 years. He is a firm believer in the interdisciplinary character of science and has diversified his interests to other fields such as mathematics, statistics, computer science, biology, genetics and linguistics. He lives with his wife Visalakshi in Chennai, India.